在学习几何的过程中,三角形全等的证明及其应用显得尤为关键,它既让众多同学感到头疼,又充满挑战。这其中不仅蕴含着巧妙的解题方法,还涉及对图形细致观察和挖掘已知条件的小技巧。
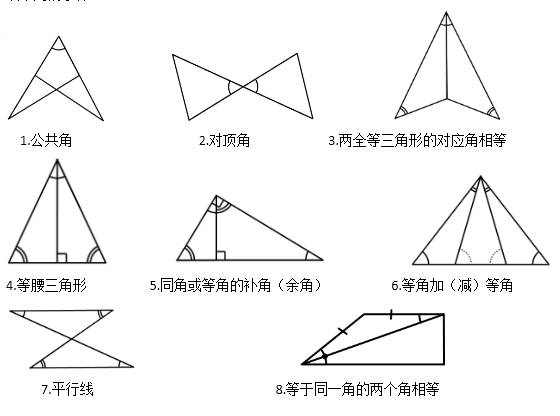
挖掘可能全等三角形

证明线段或角相等时,从结论出发,寻找可能的全等三角形,往往能收到奇效。例如,当题目中给出平行线或角平分线等条件时,我们便能在这些条件基础上构建出可能的全等三角形。如题中AB平行于CD,BE平分角ABC,CE平分角BCD,且点E位于AD上,要证明BC等于AB加CD,这时构建合适的三角形来寻找全等关系,便是解题的关键。又如,已知角BAD等于角DAC,AB大于AC,CD垂直于AD于点D,且H是BC的中点,此时,延长CD交AB于点E,以得到全等三角形,这也是运用这种思路的一个例证。
解题过程中,图形中的条件有时不易察觉,因此我们必须对图形进行详尽的分析。必须搞清楚已知条件能帮助我们建立何种等式或全等关系,绝不能随意尝试。

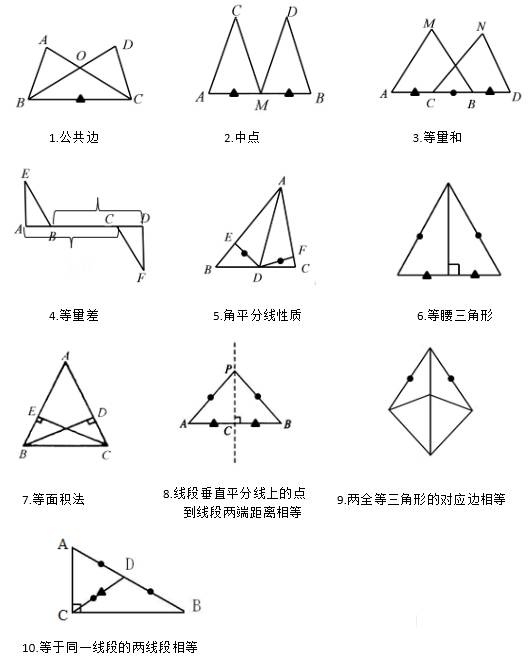
构建特殊三角形辅助解题

我们有时会利用辅助线构建特殊三角形,比如等腰三角形,来辅助解答三角形全等的问题。比如,在角平分线OC上选取一点E,然后从E点作出角OA一边的平行线DE,目的是为了构造等腰三角形ODE。再如,在角的一边OB上选取一点D,作出角平分线OC的平行线DH,并与另一边AO的反向延长线相交于点H,这样就能构造出等腰三角形ODH。这两种方法都是为了创造更多已知条件,便于证明三角形全等或求解其他未知量。
这些特殊三角形的构建方法需根据题目中的具体图形和条件来灵活应用。并非所有题目都适用于同一种构建方式。需通过不断练习来积累经验,以便在遇到类似条件时,能迅速想到如何绘制辅助线来构建特殊三角形。
证明不等关系的策略
三角形中线段的不等关系,比如在解决AB加AC大于BD加DE加CE这类问题时,我们可以使用延长线段来构建新的三角形。比如,将BD延长至与AC相交于点F,将CE延长至与BF相交于点G。接着,在三角形ABF、GFC和GDE中,运用三角形三边的关系来进行证明。这种方法的要点是,通过合理延长线段来构建相关三角形,并将需要比较的线段置于这些三角形中,依据三角形边与边的关系得出结论。
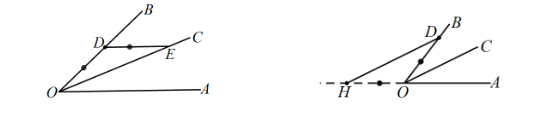
解答这类题目时,需留意延长线段的方向。必须保证延长后能成功构造出满足条件的三角形,同时能与已知条件相衔接。否则,极易陷入困境,难以得出正确答案。
证明角的大小关系
在证明角的大小关系时,比如要证明∠BDC大于∠BAC,我们可以选择延长线段,比如将BD延长至与AC相交于点E。这样一来,∠BDC就转变成了△EDC的外角。根据外角大于不相邻内角的性质,我们就可以进行证明了。这种方法,通过增加辅助线段来直接联系角,为解决角的大小关系问题提供了思路。
在使用此方法时,我们必须谨慎选择延伸线段的起点。必须确保延伸后,线段能与目标角准确对接,同时还要考虑是否能够简便高效地运用三角形的特性。
中线与三角形面积关系
三角形的中线把三角形一分为二,分割出的两个小三角形的面积是相等的。以AD为例,它是ΔABC的中线,那么SΔABD和SΔACD都等于SΔABC的一半,这是因为它们有相同的底和相同的高。这种中线和面积之间的联系,在解决某些难题时,能给出一种巧妙的解题方法。
在处理涉及多个三角形组合且与面积相关的题目时,中线的这一特性可被视为一个关键的已知条件。这一特性有助于我们建立等式,进而求解其他未知量。
等腰三角形相关证明
在等腰三角形ABC中,AB的长度等于AC。若在AB上截取BD,并在AC的延长线上截取CE,使得CE的长度等于BD,接着连接DE,使其与BC相交于点F。此类问题要求证明DF等于EF。解决这类问题,需要巧妙运用等腰三角形的特性,比如构建全等三角形或利用平行关系等。对于含有角平分线和特定角度的等腰三角形,解题思路也是相似的。
进行等腰三角形的证明时,必须善用其边和角特有的属性。以三角形ABC为例,其中AC等于BC,且∠B为90°,BD是∠ABC的角平分线。当要求解A点到直线BD的距离AD为a时,如何求出BE的长度,这类问题将等腰三角形的性质与多种条件交织在一起。我们需层层分析,挖掘出解题的关键线索。
在进行几何三角形全等相关问题的解答时,你是否拥有独到的解题技巧?期待大家不仅学会这些知识,还能为这篇文章点赞并转发,让更多同学从中受益。