你可能对门格海绵并不熟悉,然而,这一由卡尔·门格在1926年提出的理论,已成为现代数学和图形学等众多领域的宝贵财富。其独特的特性以及众多研究成果,都充满了无穷的吸引力。

门格海绵的诞生
1926年,卡尔·门格提出了“门格海绵”这一理念。这源自数学领域持续的深入研究。那时,数学界正寻求更多抽象且富有深意的概念。门格海绵的问世,犹如平静湖面抛入石子,激起一圈圈涟漪。这一概念的诞生并非巧合,而是当时数学思维碰撞与进步的产物,它标志着几何图形新探索领域的开启。这一既简单又复杂的概念,逐渐吸引了数学家的关注。
数学界正经历着变化与进步,此时门格海绵的诞生恰好迎合了时代对新型几何学研究的渴望。许多数学家开始对这个起初并不为人所知的领域产生兴趣,并逐渐认识到它所蕴含的巨大潜力和独到之处。这一概念在众多数学领域中崭露头角,吸引了众多研究者与探索者的目光。
独特的外观和迭代特性
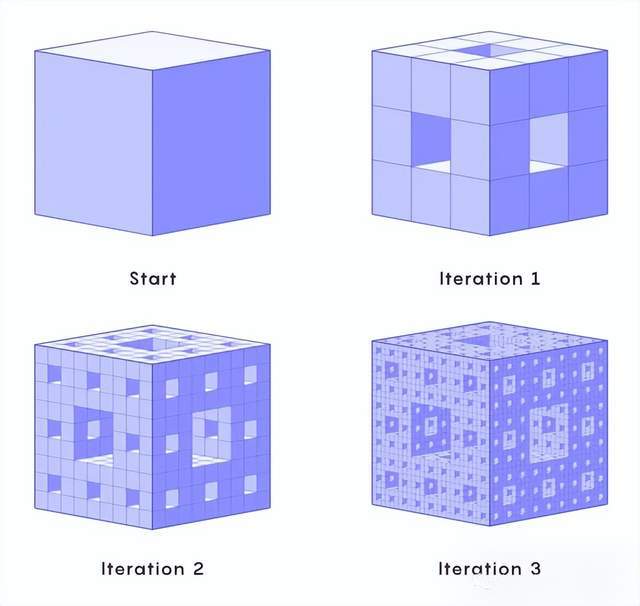
门格海绵的外观十分特别。在每次更新中,它的缝隙会以指数速度扩大,最终形态接近我们常见的海绵,这也是它名称的由来。这种独特的迭代特点,让它显得与众不同。
从基础的立方体形态起步,经过一系列的演变,它已呈现出既复杂又引人入胜的形态,与常规的几何图形有着显著的不同。以建筑行业为例,常规几何图形的使用较为局限,但门格海绵的独特特性,或许能在图形设计中催生新的可能性。其表面呈现出一种令人心动的无序美,探究这种无序之美,或许能激发对空间运用、美学设计等方面的更多思考。
计算机图形学作为一门新兴领域,其发展过程中,门格海绵的独特形态与迭代特性提供了诸多灵感。这一特性为图形渲染等技术的创新提供了新方向,并能够呈现出别具一格的视觉体验。

特殊的数学性质
门格海绵的数学特性颇为独特。在迭代过程中,其体积逐渐缩小直至为零,而表面积却不断膨胀,趋向无穷。这种特性与我们对常规几何物体体积和表面积关系的理解是相悖的。
在进行数学建模的相关研究中,这一特性会对我们的思路带来极大的影响。以物理现象模拟为例,体积与表面之间的关系通常有既定的预期,然而门格海绵的出现却促使我们重新审视这一关系。实际上,历史上众多数学概念的进步,正是由于这种颠覆传统的特性而不断前进。
研究曲线嵌入时,门格海绵展现出非凡功效。无论是直线、圆圈,还是树形、雪花等复杂图案,都能在海绵中找到相应的嵌入方法。这种特性使门格海绵成为“通用曲线”的代表,这在拓扑学领域是一次重大突破,为曲线间关系的研究开辟了新的路径。
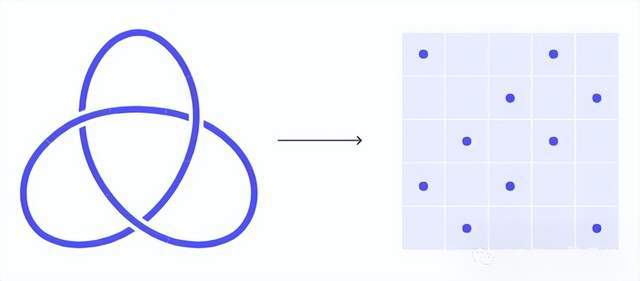
绳结的嵌入研究
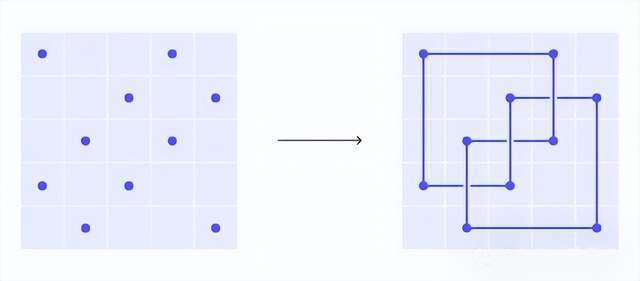
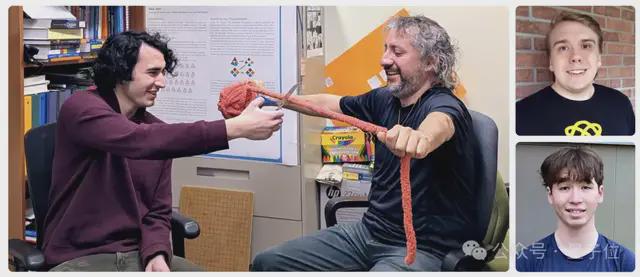
门格海绵与绳结之间存在着一种神奇的联系。例如,三叶结等“普雷策尔结”可以被对应到门格海绵的四面体形态。起初,让学生证明绳结能嵌入门格海绵,简直就像是在讲述神话故事。
学生们从学习的弧表示法入手,开始了一段探索之旅。他们先绘制绳结的图表,然后将这些图表与门格海绵的面联系起来。尽管这一过程充满挑战,他们得面对那些冗长且复杂的线图,且每一步都充满未知,但他们最终找到了解决问题的方法。在康托尔集的启发下,他们继续深入,比如对齐绳结弧线所表示的角坐标等。这一过程展示了研究思维从简单到复杂的演变。
这种对绳结嵌入的研究,并不仅限于学生的兴趣探索。在更高级别的拓扑学研究中,它具有重大价值。它可能有助于创新数学工具,也可能有助于探索更为复杂的几何联系。
学生的探索与研究启发
高中挑选学生投身于这么深奥的数学探究,实属勇敢之举。这些学生并不满足于仅仅掌握现成的证明方法,他们渴望更进一步地探索。面对繁复的数学难题,他们以单纯而坚定的态度投入其中。
研究过程中,学生们遭遇了不少挑战。他们曾误判可能与否,面临重重困难。然而,他们成功跨越了这些障碍。他们的研究方法或许能为分形复杂性的测量带来新的视角。这一案例表明,在学术研究中,新颖的思维往往能带来意外的发现。这应促使教育界深思,对学生们的探索精神和创新思维给予更多信任和激励。
未来研究的展望</u
研究已经进展到这一步,然而,仍有许多未知领域亟待我们去发掘。比如,他们还在寻找答案,看是否所有结都能被纳入门格海绵的四面体模型之中。
数学领域内,还有许多类似的新概念等待我们去探索和深入研究。门格海绵的研究成果或许能被应用于其他分形领域,探索分形结构以及更多数学关系的未知领域。你对这种持续发展的数学研究有何期待?欢迎留言分享你的看法。同时,点赞和转发这篇文章,让更多的人认识这个神奇的门格海绵。